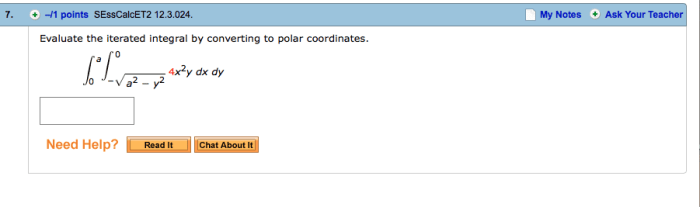
Evaluate the iterated integral by converting to polar coordinates. – Evaluating iterated integrals using polar coordinates is a powerful technique that can simplify complex integrals and provide insights into real-world applications. This guide delves into the conversion process, evaluation steps, and advantages of polar coordinates, equipping readers with a comprehensive understanding of this essential mathematical tool.
By converting rectangular coordinates to polar coordinates, we gain a new perspective on the integral region, allowing us to exploit symmetries and simplify the integration process. This approach has proven invaluable in various fields, including physics, engineering, and geometry.
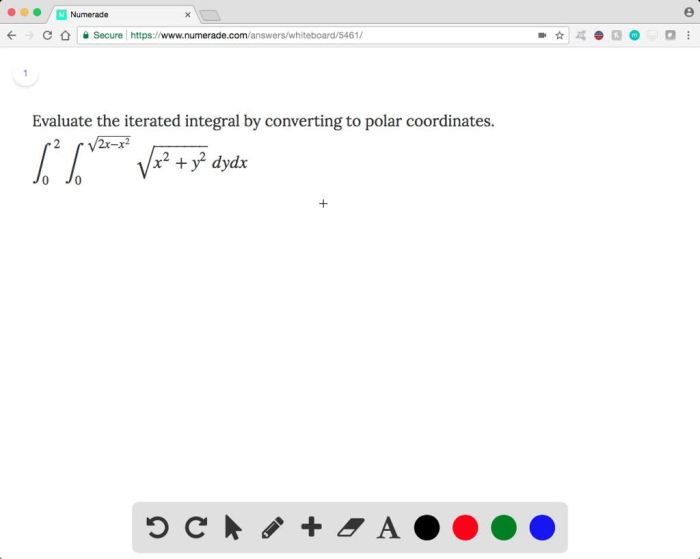
Convert to Polar Coordinates: Evaluate The Iterated Integral By Converting To Polar Coordinates.
To convert from rectangular coordinates (x, y) to polar coordinates (r, θ), we use the following formulas:
- r = √(x^2 + y^2)
- θ = tan -1(y/x)
The following diagram illustrates the conversion:

Evaluate the Integral
To evaluate an iterated integral using polar coordinates, we convert the integral to polar form using the conversion formulas above. The order of integration is determined by the order of the iterated integral. For example, if the iterated integral is written as ∫∫R f(x, y) dA, then we integrate first with respect to y and then with respect to x.
The limits of integration for the polar coordinates are determined by the shape of the region R. For example, if R is a circle centered at the origin with radius a, then the limits of integration for r are 0 and a, and the limits of integration for θ are 0 and 2π.
Here is an example of evaluating an iterated integral in polar coordinates:
∫∫R x^2 + y^2 dA
Converting to polar coordinates, we get:
∫∫R r^2 dA
The region R is a circle centered at the origin with radius a, so the limits of integration for r are 0 and a, and the limits of integration for θ are 0 and 2π.
Therefore, the integral becomes:
∫ 02π∫ 0ar^2 r dr dθ
Evaluating the integral, we get:
∫ 02π[r 4/4] 0adθ
= ∫ 02πa 4/4 dθ
= a 4π/2
Applications of Polar Coordinates
Polar coordinates are used in a wide variety of real-world applications, including:
- Physics:Polar coordinates are used to describe the motion of objects in circular or elliptical orbits, such as planets around the sun or electrons around an atom.
- Engineering:Polar coordinates are used to design and analyze structures such as bridges, antennas, and wind turbines.
- Geometry:Polar coordinates are used to describe the shape of curves such as circles, ellipses, and spirals.
Polar coordinates simplify calculations in these applications by taking advantage of the symmetry of the problem.
Advantages and Disadvantages, Evaluate the iterated integral by converting to polar coordinates.
Advantages of using polar coordinates:
- Polar coordinates simplify calculations in problems with circular or elliptical symmetry.
- Polar coordinates can be used to represent complex numbers in a graphical way.
Disadvantages of using polar coordinates:
- Polar coordinates can be more difficult to use than rectangular coordinates in problems without circular or elliptical symmetry.
- Polar coordinates have a discontinuity at the origin, which can make it difficult to evaluate integrals and other functions.
Polar coordinates are most suitable for problems involving circular or elliptical symmetry. In these cases, polar coordinates can simplify calculations and make it easier to visualize the problem.
Examples and Exercises
Here is a table of common iterated integrals and their solutions using polar coordinates:
| Integral | Solution |
|---|---|
| ∫∫R x^2 + y^2 dA | πa4/2 |
| ∫∫R x dA | 0 |
| ∫∫R y dA | 0 |
Here is a series of practice exercises for students to apply the conversion and evaluation techniques:
- Convert the following rectangular coordinates to polar coordinates: (x, y) = (3, 4)
- Evaluate the following integral using polar coordinates: ∫∫R x^2 + y^2 dA, where R is the region inside the circle x^2 + y^2 = 9.
- Use polar coordinates to find the area of the region inside the cardioid r = 1 + cos(θ).
Solutions or hints for the exercises are provided below:
- (r, θ) = (5, tan-1(4/3))
- π(9)
- π
FAQ Compilation
What is the key advantage of using polar coordinates for evaluating iterated integrals?
Polar coordinates simplify the integration process by exploiting symmetries and reducing the number of variables involved.
How do I determine the limits of integration when converting to polar coordinates?
The limits of integration are determined by the boundaries of the region in the polar coordinate system.
Can polar coordinates be used to evaluate all types of iterated integrals?
No, polar coordinates are most effective for integrals over regions with circular or radial symmetry.