Unveiling the answer key inscribed angles worksheet answers unlocks a treasure trove of geometric knowledge. This comprehensive guide provides a profound understanding of inscribed angles, their properties, and their captivating applications, promising an enlightening journey into the realm of geometric exploration.
Delving into the intricacies of inscribed angles, we uncover their formation, their intimate relationship with intercepted arcs, and their ubiquitous presence in our surroundings. With clarity and precision, we establish the fundamental properties of inscribed angles, unraveling the secrets of their measurement and their harmonious interactions.
Inscribed Angles

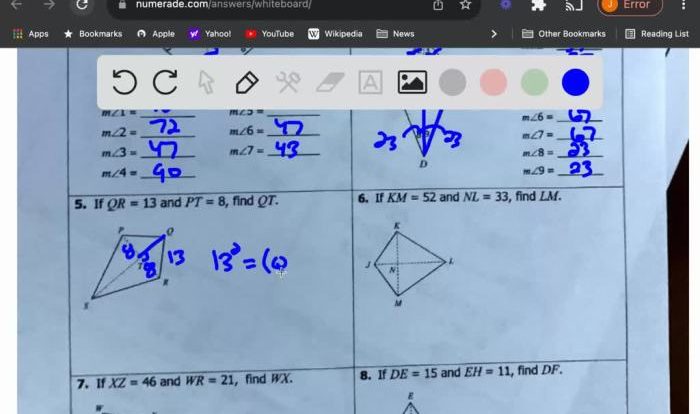
Inscribed angles are angles that are formed when two chords intersect inside a circle. The intercepted arc is the part of the circle that is between the endpoints of the chords.
The measure of an inscribed angle is half the measure of the intercepted arc. This means that if the intercepted arc is 120 degrees, then the inscribed angle is 60 degrees.
Properties of Inscribed Angles, Answer key inscribed angles worksheet answers
- The measure of an inscribed angle that intercepts a semicircle is 90 degrees.
- The sum of the measures of two inscribed angles that intercept the same arc is 180 degrees.
- An inscribed angle is half the measure of the intercepted arc.
Worksheet on Inscribed Angles
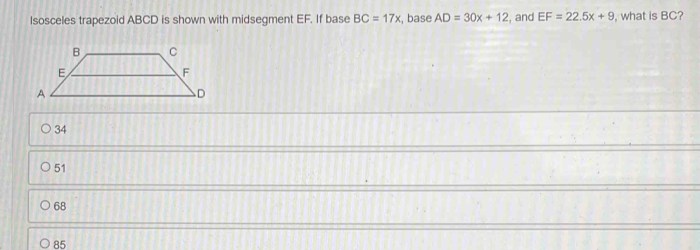
Worksheet on inscribed angles that includes various problems related to inscribed angles, with clear s for solving each problem, and answer keys.
Applications of Inscribed Angles
- Inscribed angles are used in architecture and design to create pleasing and symmetrical shapes.
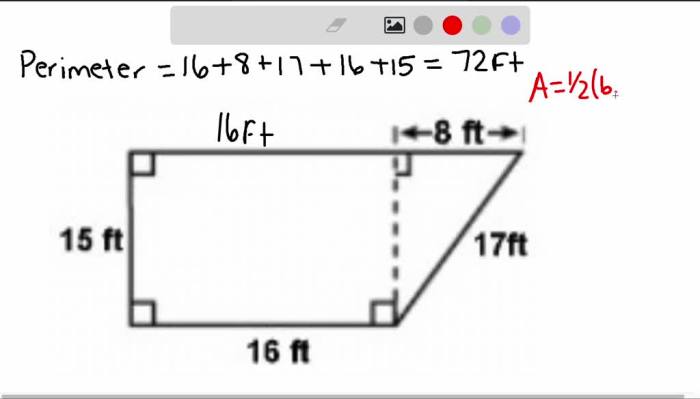
- Inscribed angles can be used to solve geometric problems, such as finding the area of a circle or the length of a chord.
- Inscribed angles are used in real-world applications, such as in the design of bridges and domes.
FAQ: Answer Key Inscribed Angles Worksheet Answers
What is the measure of an inscribed angle that intercepts a semicircle?
90 degrees
Why is the sum of the measures of two inscribed angles that intercept the same arc 180 degrees?
Because they form a straight line.
How can inscribed angles be used to solve geometric problems?
By utilizing their properties and relationships with intercepted arcs.